Naming New Puzzle Types.
The name of a puzzle should describe its most important characteristics, since creating new and different puzzle types is one of the important ways, from a teaching perspective, to keep puzzle solving fresh and useful. Although creators of Sudoku puzzles have typically limited themselves to a relatively small number of puzzle types with an ad-hoc collection of names, the goal of introducing dozens or even hundreds of new group puzzle types into common usage requires a naming convention for puzzles, such as the one described below, in which the name of the puzzle suggests some of its most important attributes.
Group Puzzle Size.
One of the most important attributes of a Group Puzzles is the size of its constraint group. For traditional Sudoku puzzles which require the placement of the values 1 through 9 exactly once in each of the 9 rows, columns, and 3x3 squares, the group size is 9. The puzzles that consist of 5 overlapping traditional Sudoku puzzles, also have a group size of 9 (even though the 5 overlapping puzzles are part of a larger 21x21 grid) because there are exactly 9 different values that must be placed in each row, column, and 3x3 square. The standard name for a traditional Sudoku puzzle in this new naming convention, therefore, would be Sudoku-9.
Group Puzzle Base Constraints.
Group puzzles of size 9 that do not require both the rows and columns to be constraint groups are not valid Latin Squares. The standard name would reflect this lack of constraints with the name Nonlatin-9. Similarly, the name Latin-9 implies that all of the rows and columns are constraint groups, but that there are no additional square constraint groups. The name Sudoku would be retained only for those puzzles that require rows, columns, and any type of rectangular constraint group that covers the entire puzzle. Thus, in the standard naming convention, any puzzle named Sudoku-N has a group size of N with all of the rows, columns, and rectangles being constraint groups.
Group Puzzle Rectangular Constraints.
Group sizes that are integer squares, such as 4, 9, 16, and up, have the obvious square constraint groups of 2x2, 3x3, and 4x4, respectively. Puzzle sizes that are not integer squares, but are even integers, can be divided into N rectangles of the same shape and orientation. These rectangles can be oriented either horizontally or vertically. The horizontal layout is considered standard and requires no addition to the standard name. The vertical layout is designated in the name by adding the word up after the size. Thus, the name Sudoku-6 indicates a puzzle that has six 3x2 horizontal rectangle constraint groups and a Sudoku-6up puzzle has six 2x3 vertical rectangles.
A more common name for a Sudoku-6 puzzle is Sudoku-Junior just as the common name for a Sudoku-9 puzzle is just Sudoku.
Some group sizes, such as 12, can be divided into either 2x6 or 3x4 rectangles. Puzzles with narrow rectangles are usually more difficult to create and solve, so the more square-like shapes are favored in the standard naming. The name Sudoku-12up, therefore, refers to a puzzle with 12 vertical 3x4 rectangles.
There is no logical limitation on creating Group Puzzles with both horizontal and vertical rectangles as constraint groups. The primary limitation is how to display the puzzles in such a way so as to show both the horizontal and vertical rectangles as constraint groups. The compromise described here appears to be the best solution: display the puzzle with the vertical rectangles outlined and the horizontal rectangles alternately shaded. If all of the horizontal rectangles were shaded, the entire puzzle would be shaded. By shading them in a checker board fashion, the horizontal rectangles are fairly clearly marked. The standard naming convention for puzzles in which both the horizontal and vertical rectangles are constraint groups is to attach the prefix "Super." to the standard name. Thus, a Group Puzzle of size 8 with both the 2x4 and 4x2 rectangles as constraint groups would be called SuperSudoku-8.
Group Puzzle Jigsaw Shapes.
Group sizes that are neither integer squares nor even integers cannot be divided into N identical rectangles, so some other shapes must be devised. The simplest solution is to use irregular contiguous jigsaw-puzzle shapes. There are many ways to divide squares into jigsaw shaped pieces of size N. One possible set of jigsaw puzzle shapes is illustrated for the Sudoku-5 puzzle shown here.
Not all possible divisions into jigsaw-puzzle type shapes, however, result in puzzle types that have any solutions. In general, the shapes cannot overlap any particular row or column in too many cells, or the resulting puzzle definition has few or no solutions that can be turned into puzzles. Because there are so many possible jigsaw puzzle shapes, multiple types of jigsaw puzzles may be defined for a particular group size. The naming convention for these additional puzzles of the same size is to add an additional letter following the standard name. For example, the following Sudoku-5B puzzle has a different set of jigsaw puzzle shapes from the previous Sudoku-5 puzzle as shown here.
The letter 'B' is used in this name because it is assumed that the initial jigsaw puzzle of the particular size is the 'A' puzzle. The third variant of size 5 would be named Sudoku-5C, etc.
Group Puzzle Diagonal Constraints.
One fairly common addition to the the standard row, column, and rectangular constraint groups is to add the diagonals of a square of size N as constraints. The two diagonals represent constraints in addition to the other constraints, even though there are only two diagonals and not every cell is a member of a diagonal constraint. The standard naming convention is to add the suffix "-X" to a base puzzle type. For example, a Sudoku-9-X or Sudoku-X puzzle is a standard Sudoku puzzle of size 9 with the addition of both diagonals as constraint groups.
In order to visually show the presence of the diagonals as a constraint group, they are usually shaded, as shown below. The naming convention of adding an 'X' to the puzzle name is because the two shaded diagonals look like the letter X. Adding both diagonals to many puzzles smaller than size 8 results in a puzzle definition that has no valid answer grids that can be made into puzzles. For some of these, a single diagonal can be added to produce puzzles. The standard naming convention for puzzles with a single diagonal rather than both diagonals is to append a 'D' to the name rather than an 'X'.
Additional Group Puzzle Rectangular Constraints.
Another way to define puzzles with additional group constraints is to have interior shapes that overlay several of the standard rectangles or squares of an existing puzzle. These puzzles are named by adding a prefix of "Hyper" to the standard puzzle name, following the pattern set by the most common puzzle of this type, the HyperSudoku puzzle. The HyperSudoku puzzle, shown below, derives its name from the fact that it adds a fourth constraint group to the usual three constraint groups of a traditional Sudoku puzzle, just as a hypercube adds a fourth dimension to the normal three dimensional of a traditional cube.
There are many different types of interior shapes that can be chosen for various types of Hyper-Sudoku puzzles. As usual, the most difficult part is to design the puzzle in a way that clearly indicates which cells are in a group. Most often this is done using shading.
For example, the HyperSudoku-12 puzzle has four 4x3 interior rectangles and one 6x2 rectangle, all shaded gray to show their location. Like diagonals, adding too many interior rectangular constraints or not overlapping the interior shapes over enough other puzzle constraint groups can severely limit or eliminate the number of possible completed grids that can be turned into puzzles.
Overlapping interior shapes can be logically defined and implemented, but the problem is finding ways to express the constraint groups clearly to the solver. One way to show an additional overlapping set of interior shapes, is to use an additional shade of gray, another color, or a shading pattern for the second set of constraint groups. All such indicators, however, must be clearly distinguishable by the solver even when the groups overlap. The HyperSudoku-X puzzle is one such puzzle with two different overlapping shaded constraint groups. A HyperSudoku-X puzzle combines the constraint groups of a HyperSudoku and a Sudoku-X puzzle, as the name implies.
Non-Contiguous Group Puzzle Constraints.
A non-contiguous constraint group has group elements that are not immediately next to each other in the puzzle, such as the outside corners of a Sudoku-4 puzzle.
In this puzzle, the non-contiguous outside corners of the puzzle form a constraint group in addition to the contiguous 4-element rows, columns, and 2x2 squares. No standard naming convention for non-contiguous groups has been defined, as yet, and ad-hoc abbreviations for the non-contiguous groups is recommended. Thus, the Sudoku-4 puzzle in which the outside corners also make up a constraint group, the name is chosen to be Sudoku-4-OC. The most common way to show this is to use a single color or shade of gray to indicate that the cells of the same shade belong to the same group. In cases where the non-contiguous group follows a clear enough pattern, such as the upper right corners of every rectangle, the group members may be outlined rather than shaded. For example, the following puzzle is named Sudoku-6up-UR-D because the base puzzle is a Sudoku-6up with the additional constraints that the upper-right corners of the rectangles are a constraint group, as is the single descending diagonal.
Signature Puzzles.
A signature puzzle is a standard Group Puzzle type in which the usual sequence of numbers, or letters for the larger puzzles, are replaced with a specific set of letters or numbers that spell out a word or message.
One singularly appropriate signature puzzle for educational purposes, is one that is created using a traditional Sudoku puzzle and substituting the letters that make up the word "EDUCATION" for the digits 1 through 9. If a puzzle were created randomly using these letters, however, there is little chance of the word "education" appearing anywhere in the puzzle. So, for a signature puzzle to be recognized as such, the word should appear in order in one of the constraint groups. The first row of the puzzle is the most prominent location to place the word or phrase when creating a signature puzzle.
The signature, however, can be placed in other prominent places, such as the first column, or any constraint group of any type of puzzle.
In fact, a signature can be place in more than one spot in a puzzle. Placing the signature in more than one spot in a puzzle, however, can be challenging for two reason. First, it is difficult in most puzzles to place a signature that is readable in two different constraint groups that does not violate the group constraints of the puzzle.
For example, you may want to place the signature in both the first column and the first row. This is not possible using any of the Group Puzzles that have the traditional Sudoku constraint groups consisting of all rows and columns because it results in duplicate letters in the first rectangle. However, in some groups of certain types of puzzles, such as HyperSudoku puzzles, it can be done.
Quilted Puzzles.
New types of Group Puzzles can be created by overlapping more than one of the smaller Group Puzzles.
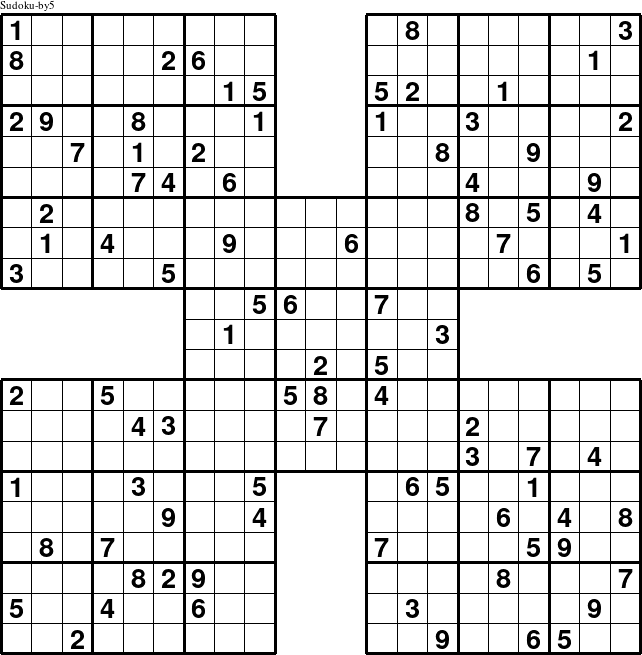
By overlapping smaller compatible puzzle types these larger puzzles are quilted together. The simplest way to ensure that the smaller quilted puzzles types are compatible is to make sure that they all use the same set of symbols as the constraint group for the quilted puzzle. The most common type of quilted puzzle is the set of five overlapping traditional Sudoku puzzles often found in the Sunday newspapers under a variety of different names. In the standard naming convention, it is called Sudoku-by5 because the base type of puzzle is a Sudoku and there are five overlapping puzzles.The smaller puzzles do not need to be the exact same type of puzzle, as illustrated by the Sudoku-Xtreme puzzle type which consists of 4Sudoku-X puzzles linked together with a single traditional Sudoku puzzle. Signature puzzles can be derived from quilted puzzles as easily as from regular non-quilted puzzles with the added advantage that the signature word can easily be placed in at least one constraint group in each of the smaller Group Puzzles, enhancing the overall effect.